Und mit anderen Worten? Verstehe nur Bahnhof. Hat zu viel Fachchinesisch im Text. Sorry
Specu braucht Unterstützung in Mathe
- Bearbeitet
Sagen wir Mal du hast eine Funktion, bei dem du einen Wert für x einsetzen kannst und einen Wert für y bekommst. Es kann vorkommen, dass du nicht für jedes mögliche x ein y-Wert bekommst, weil vielleicht dann durch 0 geteilt werden würde. ZB. bei der Funktion y = 3/(x-2) ist die Funktion bei x = 2 nicht definiert, da 3/(2-2) = 3/0 ist. Bei solchen Fällen entsteht eine Lücke in der Funktion.
Bei solchen Lücken wird es interessant zu fragen, wie es in der Nähe der Lücke aussieht, also ob die Funktion rechts und links davon für y gegen unendlich geht, oder vielleicht gegen einen bestimmten Wert.
Warum das interessant ist, kann je nach Situation unterschiedlich sein. Vielleicht hast du eine Funktion, die beschreibt, wie die maximale Geschwindigkeit von deinem ferngesteuerten Flieger ist in Abhängigkeit von der Masse des Fliegers, aber du weisst, dass du nie die Masse 0kg erreichen wirst, weil es dann kein Flieger mehr sein würde (wahrscheinlich gibt es geeignetere Beispiele, aber mir ist gerade nichts eingefallen). Da würde es dich vielleicht interessieren, wie es wird, wenn die Masse Nahe an 0kg ist, aber nicht ganz 0 ist, weil das unmöglich ist.
Ich hoffe diese Erklärung hilft deinem Verständnis ein bisschen. Ich habe hier noch keine Definition oder konkrete Berechnungen zu Limes geschrieben. Ich denke, dass du zuerst das Verständnis dazu brauchst was es überhaupt ist.
Ich habe auch versucht möglichst wenig Fachbegriffe zu verwenden, ich hoffe zu verstehst alles.
- Bearbeitet
Sorry Funktion versteht ich nicht und hatten wir glaube ich noch gar nicht.
Aber du hast den Nagel auf den Kopf getroffen. In der Klasse wird gar nicht erklärt was was ist. Es wird nur eine Formel gezeigt und wir sollten es ausrechnen.
Wenn du Funktionen noch nicht hattest, macht es nicht so viel Sinn über Limes zu sprechen.
Du kannst dir Funktionen als Maschinen vorstellen, dem du eine Zahl geben kannst und dann eine neue Zahl bekommst. Meistens ist eine Funktion gegeben durch eine Formel, wobei x die Zahl ist, die eingefügt wird und y die Zahl, die rauskommt. ZB. beschreibt 3x = y eine Funktion. Wenn wir bei dieser Funktion die Zahl 7 einfügen, bekommen wir 3°7 = 21 raus.
Wichtig ist noch, dass es nicht sein darf, dass für einen bestimmten x-Wert zwei verschiedene y-Werte entstehen, aber es kann sein, dass es für ein y-Wert zwei x-Werte gibt.
ZB. gibt es die Funktion y = x2 (Bemerkung: x2 = x°x). Wenn wir die Zahl 2 einfügen, bekommen wir 4. Aber wenn wir die Zahl -2 einfügen, bekommen wir auch 4. Dies wäre erlaubt, da für jeden x-Wert der y-Wert eindeutig ist. Anders herum, also y2 = x würde nicht gehen, da die Lösung für ein x-Wert nicht eindeutig ist.
Nozomanai vielen Dank
Wer kennt Exponentialgleichung?
https://de.serlo.org/mathe/2003/exponentialgleichung
Für Exponentialgleichungen würde ich dies Mal durchlesen.
Wichtig dabei ist zu verstehen, warum diese Schritte beim berechnen gemacht werden und nicht die Zahlen selbst. Ich habe zu viele Leute gesehen, die Formeln einfach auswendig gelernt haben und wenn etwas ein bisschen anders war an der Prüfung, konnten sie es nicht mehr lösen.
- Bearbeitet
Bei Folgen und Reihen steht folgende Formel:
!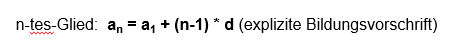
Ich weiss, dass an das gesuchte Glied ist und a1 das erste. Der Rest, keine Ahnung, wie das entstanden ist.
Ich verstehe deine Frage nicht ganz. Die ganze Folge ist dort beschrieben.
zB wäre a_1 = 4 und d = 3, dann ist die Folge
a_1 = 4 + 0°3 = 4
a_2 = 4 + 1°3 = 7
a_3 = 4 + 2°3 = 10
a_4 = 4 + 3°3 = 13
a_5 = 16, a_6 = 19, a_7 = 22, a_8 = 25, usw
Die Gleichung, die du geschrieben hast, beschriebt die ganze Folge, da n eine beliebige Zahl sein kann.
- Bearbeitet
Was ist da n-1? Was bedeutet d?
Bei Textaufgaben steht da nicht d= so und so. Dann muss ich die Zahlen zuordnen können.
ZB sei n = 7, also du betrachtest das siebte Glied der Folge, dann ist n-1 = 7-1 = 6.
Da in der Formel n-1 vorkommt, musst du für a_7 bei n-1 die Zahl 6 einfügen. Ich hoffe es wird klarer, wenn du dir die Berechnung anschaust, die ich oben geschrieben habe. Immer an der Stelle von n-1 habe ich die Zahl hingeschrieben, die um 1 kleiner ist als die Zahl des Glieds.
d ist eine Variable und sollte eigentlich für eine Aufgabe vorgegeben sein. Weil in der Formel, die du hingeschrieben hast nichts stand, habe ich einfach Mal ein Beispiel für d = 3 hingeschrieben.
Es kann gut sein, dass bei den Textaufgaben keine Variable d vorkommt. Dies war wahrscheinlich nur in der Formel, die du hier als Beispiel gebracht hast. Im Allgemeinem gibt es sehr viele verschiedene Möglichkeiten Folgen anzugeben.
Hier ist ein Beispiel: a_n = a_(n-1) + 6 falls n > 2
und a_1 = 2
Solche Angaben nennt man "rekursiv". Um a_n auszurechnen muss man a(n-1) ausrechnen, um a(n-1) auszurechnen muss man a_(n-2) ausrechnen, usw bis man bei a_1 ankommt. Hier kommt zum Beispiel kein d vor.
(Wenn ich das Zeichen "_" zwei Mal geschrieben habe, sind die Zeichen dazwischen schräg geworden und die speziellen Zeichen verschwunden, nur beim letzten Abschnitt konnte ich es nicht gut verhindern, ich hoffe du siehst wo die Zeichen wären)
Das n im a_n zeigt die Position/Stelle dieser Zahl an. d ist die Distanz zwischen der Zahl und nächsten Zahl in der entsprechenden Folge. In der Unterstufe der Schule lernt man die 2er-Reihe, 3er-Reihe usw. Bei einer 2er-Reihe ist d=2 und a_1 = 2.
Das (n-1) ist ein Produkt wo das n eingesetzt wird. z.B n=2 gibt (2-1)=1.
In deiner Formel ist a_1 der Startwert. Mit (n-1) verhindert man, dass eine Folge übersprungen wird.
Oh! Da war jemand schneller ^^
Ich habe mich in der Schule (Gymnasium) mit Mathe auch etwas schwergetan, weil es oft einfach sehr schlecht erklärt worden ist. Aus dieser Zeit stammen die Themen, die du ursprünglich genannt hast.
Heute gibts youtube videos und tolle Webseiten, aber zwei Dinge haben mir beim Verständnis damals enorm geholfen:
- Lösungswege nachprogrammieren (wenn du nachher sowieso in die Dev-Schiene willst, ist das ein super Einstieg)
- Ein CAS zum Verständnis und zur Problemlösung nutzen. Gibts auch online, z.B. hier: https://www.wolframalpha.com/
Ansonsten kann ich dir gerne beim nächsten Treffen noch meine Formelsammlung aus Schulzeiten, sowie ein Buch aus meinem Erststudium mitbringen. Fand beides damals recht hilfreich.

Nozomanai Diese Formel ist nicht von mir, die kommt vom Lehrer und ist die explizite Form und muss in der Prüfung angewendet werden.
Wie macht man das? Wie man auf die Formel kommt verstehe ich nicht.
BentoBox Danke für deine Antwort. Was ist ein CAS? Wir haben selber Formelnsammlung in Buchform bekommen. Wie Vanvelis schon geschrieben hat, nützen Formeln nichts, wenn man sie nicht versteht. Wenn der Lehrer etwas anderes möchte, muss man ja umformen können.
Ich kann vielleicht nur noch ergänzen.
Die in deinem Bild gezeigte Formel ist allgemeingültig für die sogenannte "arithmetische Folge". Das einzige was
man noch machen muss, sind Werte einsetzen oder die Formel/Gleichung nach der gesuchten Variable umformen.
Was manchmal hilft, Zahlenwerte in einem Diagramm abzubilden. Ich habe es kurz auf einem Blatt hingekritzelt.
Ähnliches gilt bei anderen Folgen, die deweils ihre eigenen Gesetzmässigkeiten haben (geometrische Folge usw.)

Specularis
Also sind alle Folgen, die du kennen musst durch die Formel gegeben, die du am Anfang hingeschrieben hast? Ich habe nur eine andere hingeschrieben als Beispiel, dass es auch andere Formeln für Folgen gibt. Wenn du aber nur solche Formeln kennen musst, kannst du das Beispiel der rekursiven Folge von mir ignorieren.
Mit deiner Frage, meinst du wie ich auf die Formel für die rekursive Folge gekommen bin? Wenn ja, kannst du es ignorieren.
Wenn wir also die Formel betrachten, die du vom Lehrer bekommen hast, ist es wie beim Bild, welches leu84 geschickt hat. Einfach gesagt kannst du dir a_1 als den Startwert vorstellen wo die Folge beginnt und d als die Schrittweite bis zum nächsten Glied. Wenn es zu mühsam ist immer wieder d dazuzurechnen bis du zum richtigen Glied kommst, kannst du auch die Zahlen n (für das n-te Glied) und d (für die Schrittweite) genau so bei den Zeichen "n" und "d" in der Formel ersetzen und ausrechnen (es ist nur Addition/Subtraktion und Multiplikation).
Alle diese Sachen wurden oben schon auf einer Art erwähnt, ich habe es nur nochmal in anderen Worten hingeschrieben. Ich hoffe es wird klarer.
Specularis
Ja genau, sonst würde es von n = 1 nach n = 2 plötzlich einen grösseren Sprung machen.


