leu84 Hallo Bento, danke für deinen Beitrag. Etwas früher ist nicht möglich, da ich den Unterricht erst am Samstag hatte. Wüsste ich früher, was kommt, könnte ich vorher fragen.
Formelsammlung habe ich schon zwei Bücher. Ich möchte nicht 1000 Bücher mit rumschleppen, hast du die ISBN deiner Vorschläge? Elektronisch ist sehr schlecht, da diese in der Prüfung nicht verwendet werden dürfen. Es dürfen je nach Berechnung nicht mal den Taschenrechner verwendet werden, ausser zur Kontrolle.
Danke für dein Screenshots, leider bringt mir das nichts, da ich nicht weiss, was mir das sagen soll.
Specu braucht Unterstützung in Mathe
Zu Funktionsklassen:
Ich denke BentoBox meint, eine Funktionsklasse wie quadratische Gleichung, log(x) oder ex. Die Funktion hat immer ein ähnliches Bild im Diagramm.
Z.B. Logarithmus log(x) funktionieren immer ähnlich. Es gibt so spezielle log-Funktionen zum Beispiel mit Potenzen (x3) und die laufen immer nach demselben Schema ab. Oft kann man diese irgendwie kürzen / vereinfachen / streichen. In den Formelsammlungen sind diese Schemas oft aufgelistet. Mit etwas Übung kennt man gewisse Eigenschaften dieser Funktionsklasse.
leu84 Sorry Leu, hab zu dir Bento geschrieben.
Von Diagrammen möchte ich gar nicht reden, da ist dann das Durcheinander perfekt. Das Problem ist, dass für Formelsammlung die Zeit fehlt. Wir bekommen sehr viel Stoffe auf sehr kurzer Zeit. Daher würde mir mehr helfen, wenn du ISBN Nummern hast von deinen Vorschlägen.
Frag deinen Lehrer was alles im Curriculum steht für dieses und evtl. die nächsten Jahre. Dann kannst du dir einen Lernplan machen. Wie Leu schon sagte: wenn die Grundlagen fehlen, dann geht das nicht einfach von heute auf morgen.
Grundsätzlich solltest du die Materie verstehen und damit umgehen können. Dafür ist es wichtig dass du alle Hilfsmittel einsetzt, die du zur Verfügung hast. Nachher für die Prüfung musst du "nur" noch den Teil des Rechnens zusätzlich übernehmen - dafür kannst du dann gesondert üben ohne die üblichen Hilfsmittel.
Ein Bild der Formelsammlung habe ich oben gemacht. Die ISBN ist: 3-87919-372-X. Allerdings war das, wie erwähnt, vor 20 Jahren. Ich würde dir fast raten eine Buchhandlung aufzusuchen und dir dort mal verschiedene Exemplare anzuschauen. Dann kannst du selbst entscheiden, was für dich funktioniert.
Soweit ich gesehen habe, gibt dir Photomath auch eine Schritt-für-Schritt Anleitung. Welchen Teil des Lösungsweges genau verstehst du nicht?
Und welchen Teil von Daniel Jungs Erklärung hast du jetzt nicht verstanden?
Das Video war jetzt auch nur ergänzend gedacht: Sobald du im Logarithmus nur noch die Variable hast, kannst du die Gleichung einfach mit Hilfe der Formelsammlung auflösen.
Funktionsklassen hat Leu schon beschrieben. Ich würde einfach von vorne anfangen, z.B. auch quadratische Funktionen vor Logarithmusfunktionen angehen. Und immer schön ausplotten, dann siehst du auch wie die Funktionen generell aussehen und ob deine Ergebnisse und Lösungswege plausibel sind.
Desweiteren würde ich auch über die regelmäßige Inanspruchnahme einer gezielten Mathe-Nachhilfe nachdenken, gerade wenn es dir schwerfällt, selbstständig nach Lösungen zu suchen und die üblichen Materialien (Bücher, youtube etc.) zu verstehen.
- Bearbeitet
Nachhilfe kostet, ich bezahle schon die Schule. Ich wüsste auch nicht, wann ich die nehmen soll.
Der Lehrer bekommt die Infos auch erst kurz am Anfang des Semesters. Ausserdem korrigiert er den Plan ständig.
Die Zeit ist wie gesagt sehr knapp. Ich habe noch diverse andere Fächer, die ich angehen muss. Bis ich es verstehe ist die Ausbildung vorbei.
Quadratische Funktionen hatte ich übrigens auch nicht verstanden. Ich denke wir haben den gleichen Lehrer von 1. bis letzten Semester. Von Anfang an war es schwierig mit ihm.
BentoBox 3-87919-372-X gibt es immer noch. Hab es mir bestellt.
Ich weiss, was das Problem ist, fällt mir heute wieder auf. Der Lehrer erklärt kein Theorie. Er fängt bei neuem Stoff bereits an zu rechnen.
Liebe Akkus, ich würde gerne diesen Thread für Mathefragen behalten, auch wenn die Prüfung vorbei ist. Danke für eure Unterstützung.
Wer kann Wahrscheinlichkeit erklären?
Specularis kann ich, aber frühestens heute Abend.
Specularis Was willst du genau über Wahrscheinlichkeit wissen? Ich hatte das Thema sehr theoretisch, aber so wie ich deine bisherigen Fragen gesehen habe, scheint das nicht so bei dir zu sein. Hast du vielleicht ein Beispiel welches du nicht verstehst?
Es gibt Permutation, Variation, Kombinationen. Ich weiss nicht, wann ich welche Formeln nehmen muss. Die sehen sich alle so ähnlich.
Specularis Ich weiss nicht welche Formeln du dazu hast, aber ich werde hier Mal ein paar wichtige Sachen hinschreiben.
Zuerst zu Permutation:
Sagen wir Mal du hast 10 verschiedene Sachen. Du hast diese Sachen irgendwie hingestellt, also es hat irgendeine Reihenfolge. Eine Permutation auf diese 10 Sachen ist eine Umordnung dieser Sachen. Also das Objekt, welches an dritter Stelle war, könnte neu an zweiter Stelle sein, usw.
Auch wenn alle Sachen nach der Permutation wieder an gleicher Stelle sind, zählt es als Permutation.
Die Anzahl möglicher Permutationen ist direkt berechenbar aus der Anzahl Objekte, und zwar sind es n! (also n°(n-1)°(n-2)°...°3°2°1) mögliche Permutationen, wobei n die Anzahl Objekte ist. Warum es so viele mögliche Permutationen hat, sieht man schnell, wenn man dies Schritt für Schritt betrachtet.
Du nimmst irgendein Objekt aus deiner Menge und gibst ihm einen neuen Platz, für den neuen Platz hast du n Orte zur Auswahl. Für das nächste Objekt hast du dann nur noch n-1 Orte zur Auswahl, dann n-2, n-3, usw. bis du dem letzten einen Platz gibst. Diese Möglichkeiten werden multipliziert und schon hast du die Formel für n!
- Bearbeitet
Specularis
Zu Variation:
Diesen Begriff habe ich vorher noch nie gehört und musste daher ein bisschen nachschauen, aber ich denke es hat damit zu tun, wie viele Möglichkeiten du im Baumdiagramm hast bei einer gleichmässigen Verteilung und beim Ziehen von k Elementen.
Wenn du die oben geschriebene Beschreibung nicht verstanden hast, ist es nicht schlimm, ich schreibe es jetzt genauer hin. Die Situation ist die Folgende: Du hast einen Behälter mit Kugeln drin, auf denen Zahlen stehen (alle Zahlen sind verschieden voneinander). Nehmen wir zum Beispiel an, dass die Anzahl Kugeln 35 ist mit den Zahlen 1 bis 35 darauf.
Wir machen zwei Experimente.
Im ersten Experiment nehmen wir k Kugeln aus dem Behälter und überlegen uns wie viele möglichen Ergebnisse es dafür geben kann. Für die erste Kugel hast du 35 Möglichkeiten, für den zweiten nur noch 34, weil die erste Kugel schon draussen ist. Für den dritten dann 33, usw. bis du k Kugeln gezogen hast. Sei k z.B. 5, dann wäre die Variation 35°34°33°32°31. Allgemein ergibt sich daraus die Formel n!/(n-k)!.
In zweiten Experiment legen wir jedes Mal, nachdem wir eine Kugel gezogen haben, die Kugel wieder zurück, damit wir immer 35 mögliche Kugeln zum ziehen haben. Bei diesem Experiment haben wir für die erste Kugel 35 Möglichkeiten, für den zweiten wieder 35, usw. bis wir k Kugeln gezogen haben. Für k = 5 wäre das 35°35°35°35°35 = 355. Im Allgemeinen ist die Formel nk.
Natürlich müssen es keine Kugeln und Behälter sein, es kann sein, dass du eine Aufgabe kriegst, bei dem du die möglichen Kombinationen beim würfeln von 3 Würfeln betrachten musst, dann ist es die gleiche Idee (63 ist die Variation in diesem Fall).
Hallo Specu
Vielleicht kann dir diese Tabelle helfen. Es ist aus einer Folie aus meiner Wahrscheinlichkeit und Statistik Vorlesung, welche ich belegt hatte.

Ein Hinweis: Das Ausrufereichen heisst in der Mathematik "Fakultät". Es wird eine Zahlenfolge miteinander multipliziert (mal-Rechnung)
Z.B.
3! = 1 * 2 * 3
6! = 1 * 2 * 3 * 4 * 5 * 6
Specularis
Zu Kombination:
Hier hat man wieder zwei Fälle. Im ersten Fall hat man n Sachen und man will k Sachen davon nehmen. Die Anzahl Möglichkeiten von n Sachen k zu nehmen ist gegeben durch "n tief k" (die Formel unter "Lotto" beim Bild von Leu84). Wenn du dir anschaust wie "n tief k" definiert ist, merkst du vielleicht, dass der Teil oberhalb vom Bruchstrich die Formel bei der Variation ist, da diese Formel ja angibt wie viele Möglichkeiten es gibt k Sachen aus n Sachen zu nehmen. Der Teil unter dem Bruchstrich macht, dass die Formel den Fall, dass wir z.B. zuerst das Objekt 1 ziehen und dann das Objekt 7 ziehen, gleich macht zum Fall, dass wir zuerst Objekt 7 ziehen und dann Objekt 1 ziehen. Also am Ende sollte es nur darauf ankommen was man zieht und nicht in welcher Reihenfolge.
Der zweite Fall legt wieder die Objekte zurück, bevor man erneut zieht. Also es ist möglich das gleiche Objekt mehrmals zu ziehen. Diese Formel ist sehr ähnlich zum ersten Fall, man betrachtet einfach den den Behälter als um k-1 vergrössert, damit man am Ende noch n-1 Objekte übrig hat.
- Bearbeitet
Dieses Mal konnte ich in der Schule folgen. Aber die Schwierigkeit ist, dass ich eine Textaufgabe bekomme und dann innerhalb einer Minute zu wissen, welche Formel ich anwenden soll, ist schwer.
Danke @Nozomanai und @leu84 für eure Erklärungen.
Das ist bei uns Permutation:

Das ist Variation ohne Wiederholung:
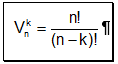
Das ist Variation mit Wiederholung:

Anzahl Kombinationen ohne Wiederholung:
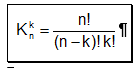
Anzahl Kombinationen mit Wiederholung:
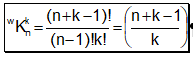
leu84 danke für die Tabelle, ich verstehe aber trotzdem nicht was Variationen, Kombinationen und Permutationen bedeuten. Ohne das Verständnis weiss ich ja nicht welche Formel nehmen.
Aus meiner Tabelle ist der Ausdruck oben in der Klammer erklärt. Trotzdem kurz ein paar Worte dazu:
Variation bedeutet, dass eine bestimmte Reihenfolge von Zahlen oder Buchstaben. Die Reihenfolge einer Zahlenkombination am Zahlenschloss oder Zeichenkombination beim Passwort sind eindeutig.
Kombination bedeutet, dass es keine bestimmte Reihenfolge gesucht wird. Zum Beispiel beim Lotto ist es egal welche Zahl in welcher Reihenfolge gezogen werden.
Permutation kann ich im Bereich der Statistik/Wahrscheinlichkeit nicht im Detail erklären. Aber ich hatte kaum Aufgaben zu Permutation in meinem Studium, soweit ich mich erinnern kann


